A. 爱丽丝的 Sweet Magic 题目描述 给定一个数组 a a a + 1 +1 + 1 ∏ i = 1 n a i \prod_{i=1}^n a_i ∏ i = 1 n a i 「YAC Round 3」爱丽丝的 Sweet Magic
解法一 暴力枚举 数据量比较小,每组数据数组大小不超过 10 10 10 + 1 +1 + 1 a i a_i a i
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <bits/stdc++.h> using namespace std;#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) typedef long long ll;int main () int T; cin >> T;while (T -- ){int n; cin >> n;vector<int > a (n + 1 ) ;for (int i = 1 ; i <= n; i ++ ) cin >> a[i];0 ;for (int i = 1 ; i <= n; i ++ ){1 ;for (int j = 1 ; j <= n; j ++ )if (i != j) prod *= a[j];max (res, prod);'\n' ;return 0 ;
解法二 贪心 我们可以假设进行 + 1 +1 + 1 a k a_k a k 1 ≤ k ≤ n 1 \le k \le n 1 ≤ k ≤ n + 1 +1 + 1 sum \text{sum} sum a k a_k a k sum \text{sum} sum a a a a k a_k a k + 1 +1 + 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <bits/stdc++.h> using namespace std;#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) typedef long long ll;int main () int T; cin >> T;while (T -- ){int n; cin >> n;vector<int > a (n + 1 , 10 ) ;int mn = 0 ; for (int i = 1 ; i <= n; i ++ ){if (a[i] < a[mn]) mn = i;1 ;for (int i = 1 ; i <= n; i ++ ) res *= a[i];'\n' ;return 0 ;
B. 迷途竹林的月色 题目描述 给定一个起点和一个终点,问网格图中是否可以从起点到达终点。(非常简单且典型的搜索模板题)「YAC Round 3」迷途竹林的月色
解法一 BFS 广度优先搜索。标准的模板题,内容较为简单,如有不熟悉该模板的可自行查找资料等进行学习。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 #include <bits/stdc++.h> using namespace std;#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) #define MP make_pair typedef pair<int , int > pii;const int dx[4 ] = {1 , -1 , 0 , 0 };const int dy[4 ] = {0 , 0 , 1 , -1 };const int N = 110 ;int n, m, sx, sy, tx, ty;char g[N][N];bool vis[N][N];bool bfs () if (g[sx][sy] == '#' || g[tx][ty] == '#' ) return false ; push (MP (sx, sy)), vis[sx][sy] = true ;while (q.size ()){auto [x, y] = q.front ();pop ();if (x == tx && y == ty) return true ;for (int k = 0 ; k < 4 ; k ++ ){int nx = x + dx[k], ny = y + dy[k];if (nx < 1 || nx > n || ny < 1 || ny > m) continue ; if (g[nx][ny] == '#' || vis[nx][ny]) continue ; push (MP (nx, ny)), vis[nx][ny] = true ;return false ;int main () for (int i = 1 ; i <= n; i ++ ) cin >> (g[i] + 1 );bfs () ? "Marisa" : "Alice" ) << '\n' ;return 0 ;
解法二 DFS 深度优先搜索
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <bits/stdc++.h> using namespace std;#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) #define MP make_pair typedef pair<int , int > pii;const int dx[4 ] = {1 , -1 , 0 , 0 };const int dy[4 ] = {0 , 0 , 1 , -1 };const int N = 110 ;int n, m, sx, sy, tx, ty;char g[N][N];bool vis[N][N];bool dfs (int x, int y) if (x < 1 || x > n || y < 1 || y > m) return false ; if (g[x][y] == '#' || vis[x][y]) return false ; true ;if (x == tx && y == ty) return true ; for (int k = 0 ; k < 4 ; k ++ ){int nx = x + dx[k], ny = y + dy[k];if (dfs (nx, ny)) return true ; return false ; int main () for (int i = 1 ; i <= n; i ++ ) cin >> (g[i] + 1 );dfs (sx, sy) ? "Marisa" : "Alice" ) << '\n' ;return 0 ;
C. 某科学的炫彩呱太 题目描述 给定一个长度为 n n n a a a q q q [ l , r ] [l, r] [ l , r ] [ l , r ] [l, r] [ l , r ] 「YAC Round 3」某科学的炫彩呱太
解题思路 思维 我们可以倒过来思考这个问题,把问题转换为:判断一个区间中是否存在一个数,其 前一个 相等的数的位置是否在当前的区间中。
可以注意到,元素大小不超过 1 0 5 10^5 1 0 5 idx \text{idx} idx idx [ x ] \text{idx}[x] idx [ x ] x x x
我们再开一个数组 mx \text{mx} mx i i i idx \text{idx} idx
对于每个询问的区间 [ l , r ] [l, r] [ l , r ] mx [ r ] \text{mx}[r] mx [ r ] 小于 l l l mx [ r ] < l \text{mx}[r] < l mx [ r ] < l l l l
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> using namespace std;#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) int main () int n, q; cin >> n >> q;vector<int > a (n + 1 ) , mx (n + 1 ) , idx (n + 1 ) ;for (int i = 1 ; i <= n; i ++ ){max (mx[i - 1 ], idx[a[i]]); while (q -- ){int l, r; cin >> l >> r;"Yes" : "No" ) << '\n' ; return 0 ;
PS: 此题也可以用莫队解决,属于进阶内容,不要求掌握,感兴趣的可以去了解了解。
D. 芙莉莲的冒险 题目描述 给定一个长度为 n n n a a a n n n t t t i i i a 1 , a 2 , … , a i a_1, a_2, \ldots , a_i a 1 , a 2 , … , a i t i t_i t i 0 0 0 min ( a k , t i ) \min(a_k, t_i) min ( a k , t i ) 1 ≤ k ≤ i 1 \le k \le i 1 ≤ k ≤ i i i i k k k 「YAC Round 3」芙莉莲的冒险
解题思路 模拟 + 前缀和 + 二分 + 差分 对于数组 a a a a i a_i a i i i i t t t a i a_i a i 0 0 0 0 0 0 t t t 前缀和 p r e pre p re 二分 查找得到每个 a i a_i a i 0 0 0 [ i , n ] [i, n] [ i , n ]
对于数组 t t t j j j a a a [ 1 , j ] [1, j] [ 1 , j ] p p p t j t_j t j s u m j sum_j s u m j p × t j p \times t_j p × t j a a a [ 1 , j ] [1, j] [ 1 , j ] < t j < t_j < t j
我们可以反过来思考,看每个元素 a i a_i a i s u m j sum_j s u m j t j t_j t j a i a_i a i j j j ≥ t j \ge t_j ≥ t j a i < t j a_i < t_j a i < t j s u m j sum_j s u m j
对于统计每个元素 a i a_i a i s u m j sum_j s u m j 差分 来记录,差分数组记为 d i f f diff d i ff a i a_i a i 0 0 0 p o s pos p os
如果 p r e [ p o s ] − p r e [ i − 1 ] < a [ i ] pre[pos] - pre[i - 1] < a[i] p re [ p os ] − p re [ i − 1 ] < a [ i ] a i a_i a i 0 0 0 [ i , n ] [i, n] [ i , n ] + 1 +1 + 1 a [ i ] a[i] a [ i ] [ i , n ] [i, n] [ i , n ] 1 1 1 t j t_j t j i ≤ j ≤ n i \le j \le n i ≤ j ≤ n
如果 p r e [ p o s ] − p r e [ i − 1 ] = a [ i ] pre[pos] - pre[i - 1] = a[i] p re [ p os ] − p re [ i − 1 ] = a [ i ] a i a_i a i p o s pos p os 0 0 0 [ i , p o s ] [i, pos] [ i , p os ] + 1 +1 + 1 a [ i ] a[i] a [ i ] [ i , p o s ] [i, pos] [ i , p os ] 1 1 1 t j t_j t j i ≤ j ≤ p o s i \le j \le pos i ≤ j ≤ p os
如果 p r e [ p o s ] − p r e [ i − 1 ] > a [ i ] pre[pos] - pre[i - 1] > a[i] p re [ p os ] − p re [ i − 1 ] > a [ i ] p o s pos p os a i a_i a i t p o s t_{pos} t p os d i f f [ i ] + + , d i f f [ p o s ] − − diff[i] ++ , diff[pos] -- d i ff [ i ] + + , d i ff [ p os ] − − [ i , p o s − 1 ] [i, pos - 1] [ i , p os − 1 ] + 1 +1 + 1 a i − ( p r e [ p o s − 1 ] − p r e [ i − 1 ] ) a_i - (pre[pos - 1] - pre[i - 1]) a i − ( p re [ p os − 1 ] − p re [ i − 1 ]) l f t lft l f t
处理完差分后,求一下 d i f f diff d i ff t j t_j t j s u m j sum_j s u m j s u m j = t j × d i f f [ j ] + l f t [ j ] sum_j = t_j \times diff[j] + lft[j] s u m j = t j × d i ff [ j ] + l f t [ j ] d i f f diff d i ff l f t lft l f t
遍历所有的 s u m sum s u m 小于 k k k
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #include <bits/stdc++.h> using namespace std;#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) typedef long long ll;const int N = 1e5 + 10 ;int diff[N]; int main () int n, k; cin >> n >> k;vector<int > a (n + 1 ) , t (n + 1 ) ;for (int i = 1 ; i <= n; i ++ ) cin >> a[i];for (int i = 1 ; i <= n; i ++ ) cin >> t[i];for (int i = 1 ; i <= n; i ++ ) pre[i] = pre[i - 1 ] + t[i]; for (int i = 1 ; i <= n; i ++ ){int l = i, r = n; while (l < r){int mid = l + r >> 1 ;if (pre[mid] - pre[i - 1 ] >= a[i]) r = mid;else l = mid + 1 ;if (pre[r] - pre[i - 1 ] < a[i]) diff[i] ++ ; else if (pre[r] - pre[i - 1 ] == a[i]) diff[i] ++ , diff[r + 1 ] -- ; else {1 ] - pre[i - 1 ]); for (int j = 1 ; j <= n; j ++ ) diff[j] += diff[j - 1 ]; 0 , mn = 2e18 ; for (int j = 1 ; j <= n; j ++ ){max (mx, sum), mn = min (mn, sum);"YES" : "NO" ) << '\n' ;'\n' ;return 0 ;
E. 星屑幻想 Stardust Reverie 题目描述 给定一颗无向树,任选三个点 A , B , C A, B, C A , B , C max ( d i s t A B + min ( d i s t C A , d i s t C B ) ) \max{(dist_{AB} + \min{(dist_{CA}, dist_{CB})})} max ( d i s t A B + min ( d i s t C A , d i s t CB ) ) 星屑幻想 Stardust Reverie
解题思路 贪心 + 树的直径 + 枚举 我们不妨假设 A A A C C C B B B C C C d i s t C A ≤ d i s t C B dist_{CA} \le dist_{CB} d i s t C A ≤ d i s t CB d i s t C A + d i s t A B dist_{CA} + dist_{AB} d i s t C A + d i s t A B
对于路径 d i s t C A + d i s t A B dist_{CA} + dist_{AB} d i s t C A + d i s t A B
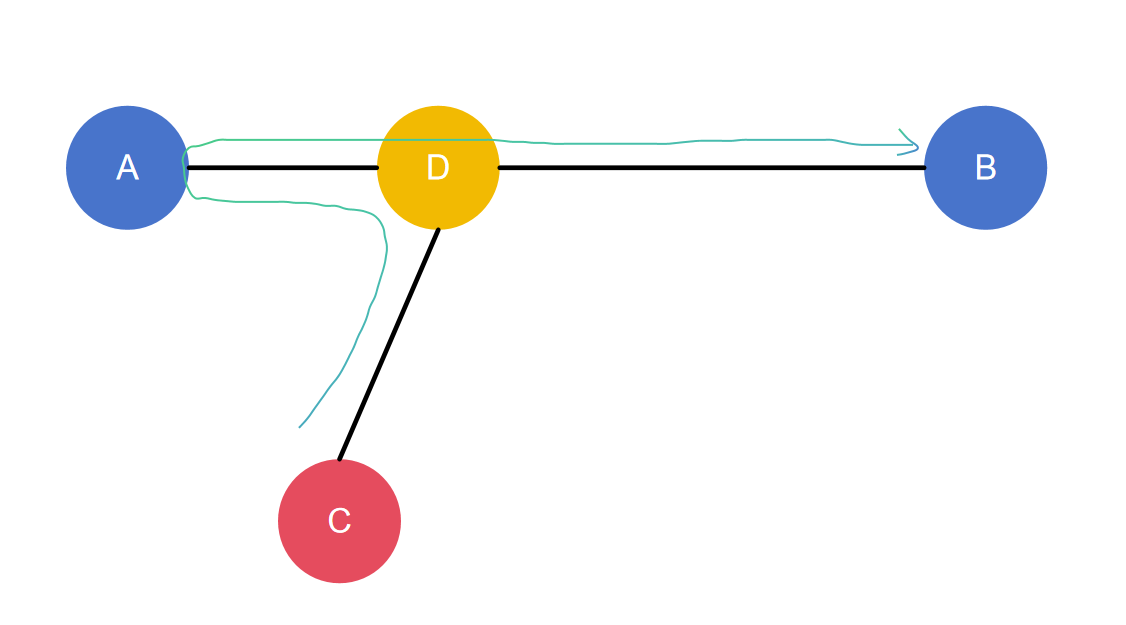
C → A C \rightarrow A C → A A → B A \rightarrow B A → B 中间部分 存在交点。
假设交点为 D D D C → A C \rightarrow A C → A D → A D \rightarrow A D → A A → B A \rightarrow B A → B A → D A \rightarrow D A → D
显然,d i s t C A dist_{CA} d i s t C A d i s t A B dist_{AB} d i s t A B 让 d i s t A B dist_{AB} d i s t A B 。由于是一棵树,最长的两点之间距离,当为 树的直径 ,因此,我们基于贪心思想得到的 A A A B B B A A A B B B
所以当前情况下的答案为 d i s t C A dist_{CA} d i s t C A + 树的直径
C → A C \rightarrow A C → A A → B A \rightarrow B A → B 中间部分 没有交点。
当前情况,表明路径就是 C → A → B C \rightarrow A \rightarrow B C → A → B d i s t C B dist_{CB} d i s t CB
所以当前情况下的答案为 树的直径 ,显然不如前面有交点的情况。
因此,我们需要先求出树的直径,得到树的直径对应的端点 A A A B B B A A A C C C min ( d i s t C A , d i s t C B ) \min{(dist_{CA}, dist_{CB})} min ( d i s t C A , d i s t CB ) 枚举树中的每个节点作为点 C C C min ( d i s t C A , d i s t C B ) \min{(dist_{CA}, dist_{CB})} min ( d i s t C A , d i s t CB ) 。
对于求树的直径,一般有两种方法,分别为 两次 d f s dfs df s 树形DP 。题解中将采用 两次 d f s dfs df s OI Wiki 树的直径 )
对于枚举的部分,我们可以从两个端点开始求出各自到其他点的树上距离,可以采用 d f s dfs df s b f s bfs b f s 双源 b f s bfs b f s A A A B B B d [ u ] d[u] d [ u ] min ( d i s t C A , d i s t C B ) \min{(dist_{CA}, dist_{CB})} min ( d i s t C A , d i s t CB ) b f s bfs b f s u u u min ( d i s t C A , d i s t C B ) \min{(dist_{CA}, dist_{CB})} min ( d i s t C A , d i s t CB ) d [ u ] d[u] d [ u ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 #include <bits/stdc++.h> using namespace std;#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) typedef long long ll;const int N = 2e5 + 10 , M = (N << 1 );int h[N], e[M], ne[M], w[M], idx;void add (int a, int b, int c) int a, b, f; void dfs (int u, int fa) for (int i = h[u]; i; i = ne[i]){int v = e[i];if (v == fa) continue ;if (dist[v] > dist[f]) f = v; dfs (v, u);void bfs () memset (d, 0x3f , sizeof d);int > q;push (a), d[a] = 0 ;push (b), d[b] = 0 ; while (q.size ()){int u = q.front ();pop ();for (int i = h[u]; i; i = ne[i]){int v = e[i];if (d[v] > d[u] + w[i]) q.push (v), d[v] = d[u] + w[i];int main () int n, m; cin >> n >> m;while (m -- ){ int u, v, c; cin >> u >> v >> c; add (u, v, c), add (v, u, c);1 ;dfs (1 , -1 ); 0 ;dfs (f, -1 ); bfs (); 0 ; for (int i = 1 ; i <= n; i ++ ) res = max (res, dist[f] + d[i]);'\n' ;return 0 ;
选取 A , B A, B A , B 我们可以通过反证法来证明选取 A , B A,B A , B
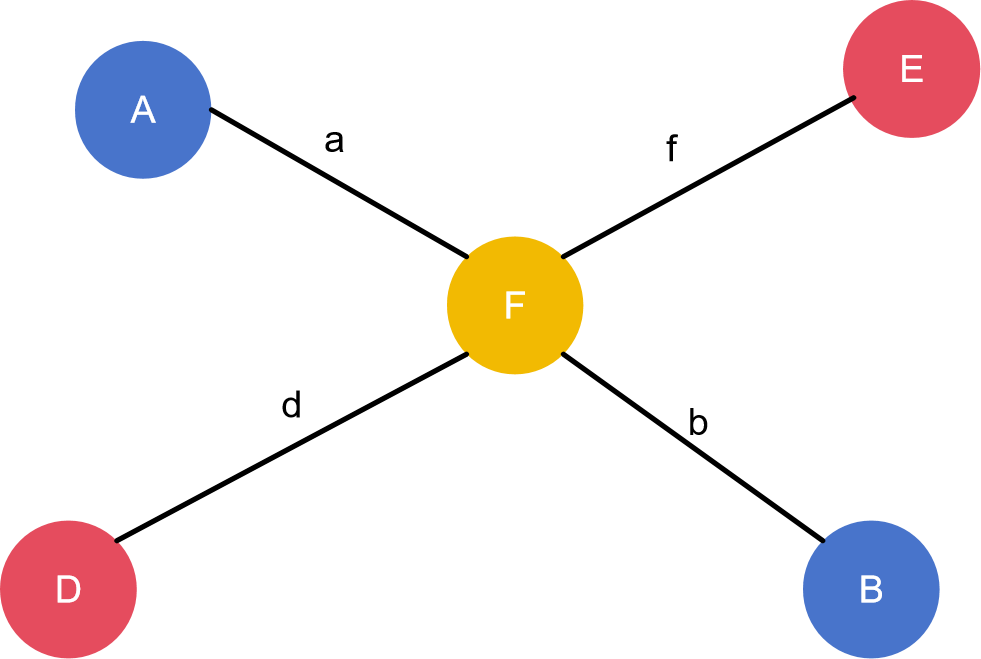
假设我们选取的 A , B A,B A , B D , E D,E D , E A A A B B B D E DE D E F F F
由于 D E DE D E A B AB A B
a + b < d + f a + b < d + f
a + b < d + f
同时,我们还不能让 A D AD A D A E AE A E B D BD B D B E BE BE
a + d < d + f → a < f a + d < d + f \rightarrow a < f
a + d < d + f → a < f
a + f < d + f → a < d a + f < d + f \rightarrow a < d
a + f < d + f → a < d
b + d < d + f → b < f b + d < d + f \rightarrow b < f
b + d < d + f → b < f
b + f < d + f → b < d b + f < d + f \rightarrow b < d
b + f < d + f → b < d
我们可以再假设 a < b a < b a < b d > f d > f d > f A , B A, B A , B D D D C C C D → F → A → F → B D \rightarrow F \rightarrow A \rightarrow F \rightarrow B D → F → A → F → B d + 2 × a + b d + 2 \times a + b d + 2 × a + b
但是,我们可以发现,如果任意选取路径 B → F → E → F → D B \rightarrow F \rightarrow E \rightarrow F \rightarrow D B → F → E → F → D b + 2 × f + d b + 2 \times f + d b + 2 × f + d a < f a < f a < f d + 2 × a + b < d + 2 × f + b d + 2 \times a + b < d + 2 \times f + b d + 2 × a + b < d + 2 × f + b A , B A,B A , B A , B A, B A , B
因此,我们反证法可以得到,选取 A , B A, B A , B
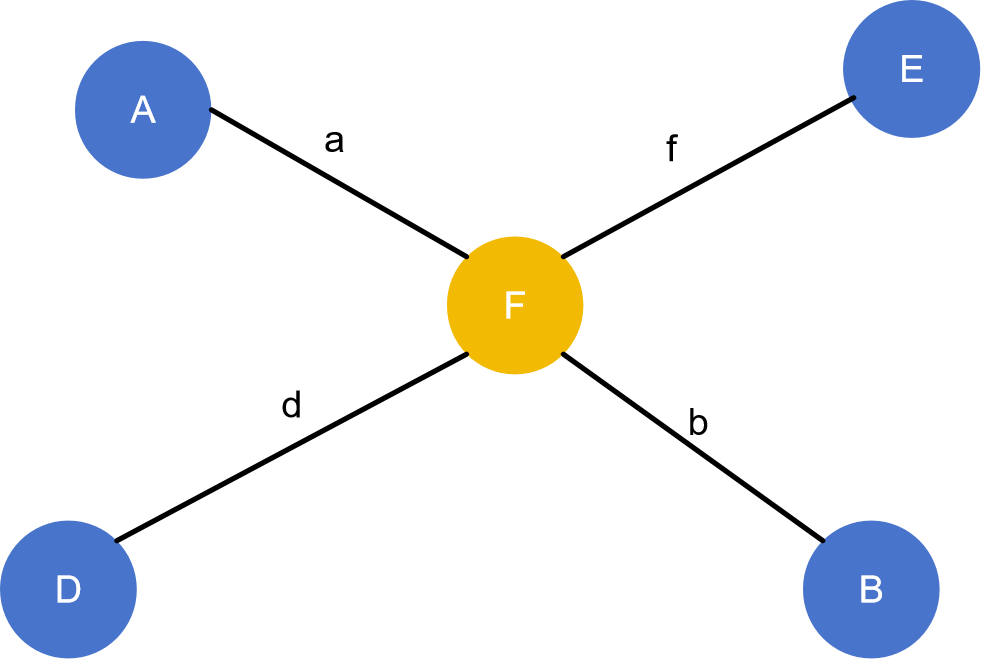
关于存在多对树的直径端点的问题 还是和前面类似的一张图,如下图所示:
我们假设 A , B A, B A , B D , E D, E D , E
a + b = d + f a + b = d + f
a + b = d + f
因为 A A A D D D ≤ \le ≤ A D AD A D
a + d = a + b = d + f a + d = a + b = d + f
a + d = a + b = d + f
由此,我们可以得出 b = d b = d b = d a = f a = f a = f
类似上面的证明,我们还可以得到 a = d a = d a = d b = f b = f b = f
a = b = d = f a = b = d = f
a = b = d = f
所以,对于存在多对树的直径端点的情况,我们可以发现,最长的路径长度一定是在 A , B , C A, B, C A , B , C 两倍的树的直径长度 (选取 C C C
因此,完全不用担心出现多对树的直径的情况,任意选取 A , B A, B A , B C C C
F. 欢迎来到雾雨魔法店 题目描述 初始情况下有 n n n a i a_i a i b i b_i b i m m m
对于操作 1 l r,则输出 [ l , r ] [l, r] [ l , r ] ∑ i = l r s i r − l + 1 \frac{\sum_{i=l}^r s_i}{r - l + 1} r − l + 1 ∑ i = l r s i s i s_i s i
对于操作 2 x y,将下标为 x x x 增加 y y y
「YAC Round 3」欢迎来到雾雨魔法店
解题思路 动态开点线段树 + 维护前缀和区间和 根据数据范围,采用一般线段树无疑会内存超限。因此我们需要进行离散化,但是本题在两种操作中都会出现先前未出现过的下标(对应题中的等级)。故如果采用离散化的技巧,我们还必须把操作中所有的下标也存起来再进行离散化,而操作又涉及区间询问,区间的离散化显然会比较繁琐,因此我们可以转而采用另外一种技巧 动态开点 。(动态开点线段树 )
因为下标数据范围,达到了 32 32 32 INF = 2147483647 \text{INF} = 2147483647 INF = 2147483647 2 31 − 1 2^{31} - 1 2 31 − 1 [ 1 , INF ] [1, \text{INF}] [ 1 , INF ]
动态开点线段树开的空间大小需要关注的是 操作次数 和 区间范围 ,注意操作次数还包括了前面初始的 n n n 2 × 1 0 5 2\times 10^5 2 × 1 0 5 log ( v ) \log(v) log ( v ) v v v 32 32 32
解决了空间问题,那么如何处理操作 1 1 1
如果每次处理操作 1 l r,把范围内的 s u m i sum_i s u m i r − l + 1 r - l + 1 r − l + 1
我们可以 维护前缀和的区间和 ,因此,我们需要将 单点修改操作转换为区间修改操作 。比如下标 x x x y y y x x x s u m x sum_x s u m x [ 1 , x ] [1, x] [ 1 , x ] x x x y y y [ x , INF ] [x, \text{INF}] [ x , INF ] y y y
也就是说,对于操作 1 l r,我们只需要输出 [ l , r ] [l, r] [ l , r ] 2 x y 以及初始化操作,我们则需要进行区间修改,将 [ x , INF ] [x, \text{INF}] [ x , INF ] y y y
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 #include <bits/stdc++.h> using namespace std;#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) typedef long long ll;const int N = 2e5 + 10 , INF = 2147483647 ; struct node {int ls, rs; ll sum, lazy;}tr[N * 32 ]; int root, tot; void pushup (int u) void pushdown (int u, int l, int r) if (tr[u].lazy){ int mid = l + r >> 1 ;if (!tr[u].ls) tr[u].ls = ++ tot;if (!tr[u].rs) tr[u].rs = ++ tot; 1 );0 ; void modify (int &u, int l, int r, int ql, int qr, ll x) if (!u) u = ++ tot; if (ql <= l && r <= qr){1 ); return ;pushdown (u, l, r);int mid = l + r >> 1 ;if (ql <= mid) modify (tr[u].ls, l, mid, ql, qr, x);if (qr > mid) modify (tr[u].rs, mid + 1 , r, ql, qr, x);pushup (u);ll query (int u, int l, int r, int ql, int qr) {if (!u) return 0ll ;if (ql <= l && r <= qr) return tr[u].sum;pushdown (u, l, r);int mid = l + r >> 1 ; ll res = 0 ;if (ql <= mid) res += query (tr[u].ls, l, mid, ql, qr);if (qr > mid) res += query (tr[u].rs, mid + 1 , r, ql, qr);return res;int n, m;int main () for (int i = 1 ; i <= n; i ++ ){ int x, y; cin >> x >> y;modify (root, 1 , INF, x, INF, y); while (m -- ){int op, x, y; cin >> op >> x >> y;if (op == 1 ) {double res = query (root, 1 , INF, x, y);printf ("%.4lf\n" , res / (y - x + 1 ));else {modify (root, 1 , INF, x, INF, y); return 0 ;