2024 YAC Round 9 题解

A 未来不可限量

题意描述

输出 “Sky is limit.”\text{“Sky is limit.”} 。https://www.luogu.com.cn/problem/T438134

解题思路

签到题。

1
2
3
4
5
6
7
8
9
10
11
12
#include<bits/stdc++.h>
using namespace std;

#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)

int main(){
    ios;

    puts("Sky is limit.");

    return 0;
}

B ⑨ 号彩票

题意描述

一个大小为 99 行 99 列的数组，每个位置有一个号码和金额。询问两个数字，求等于这两个数字的位置的金额总数。最后答案记得要减去 999999 。「YAC Round 9」⑨ 号彩票

解题思路

按照题意统计即可，注意开 long long\text{long long} 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;

#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
typedef long long ll;
const int N = 11;

int g[N][N], w[N][N], n1, n2;
ll res = -999;

int main(){
    ios;

    for(int i = 1; i <= 9; i ++ )
        for(int j = 1; j <= 9; j ++ )
            cin >> g[i][j];
    for(int i = 1; i <= 9; i ++ )
        for(int j = 1; j <= 9; j ++ )
            cin >> w[i][j];

    cin >> n1 >> n2;
    for(int i = 1; i <= 9; i ++ )
        for(int j = 1; j <= 9; j ++ )
            if(g[i][j] == n1 || g[i][j] == n2) res += w[i][j];

    cout << res << "\n";

    return 0;
}

C 在简单题寻求回文串是否搞错了什么

题意描述

求给定字符串中每个字符出现次数不超过 22 次的回文子串个数。「YAC Round 9」在简单题寻求回文串是否搞错了什么

解题思路 中心扩展法

本题求解的关键之处在于 每个字符出现次数不超过 22 次，由于只包含小写英文字符，故最长的回文串长度不会超过 26×226 \times 2（也就是每种英文字符都出现两次，且呈现对称的形式）。

因此，我们可以直接枚举每个位置，采用中心扩展法，在扩展过程中，维护每个字符出现的次数，不断向两边扩展得到回文子串的个数（由前面的结论可知，每个位置扩展次数不会超过 2626 次）。分别统计奇数长度和偶数长度的回文子串个数，累加答案即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
using namespace std;

#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)

int main(){
    ios;

    string s; cin >> s;
    int res = 0, n = s.size();

    for(int i = 0; i < n; i ++ ){ // 长度为奇数
        int cur = 1;
        vector<int> cnt(26, 0);
        cnt[s[i] - 'a'] ++ ;
        for(int l = i - 1, r = i + 1; l >= 0 && r < n && s[l] == s[r]; l -- , r ++ ){
            cnt[s[l] - 'a'] += 2;
            if(cnt[s[l] - 'a'] > 2) break;
            cur ++ ;
        }
        res += cur;
    }

    for(int i = 0; i < n - 1; i ++ ){ // 长度为偶数
        int cur = 0;
        vector<int> cnt(26, 0);
        for(int l = i, r = i + 1; l >= 0 && r < n && s[l] == s[r]; l -- , r ++ ){
            cnt[s[l] - 'a'] += 2;
            if(cnt[s[l] - 'a'] > 2) break;
            cur ++ ;
        }
        res += cur;
    }

    cout << res << "\n";

    return 0;
}

D 《东方妖精武踏会》

题意描述

游戏厅有一台游戏机，最多可以两个人同时游玩，需要维护一个队列模拟排队玩游戏。有以下三种事件：

  • start： 一局游戏开始。上一局的玩游戏的人需要 先按照原本的顺序回到队尾 以让出游戏机（前提是存在上一局游戏）。 然后，让当前队列中的 前两个人或一个人（队列里可能只有一个人） 上场，此时按照顺序输出这两个人或一个人； 若这一局游戏无人上场，则输出 Error 并忽略这个事件。

  • arrive x：xx 到达游戏厅并且加入队尾。 此时 xx 不应该在排队也不应该在游玩，若 xx 不在队列中，则事件成功执行，输出 OK；否则输出 Error 并忽略这个事件。

  • leave x：xx 离开游戏厅并离开队列。 此时 xx 应该在排队但不应该在游玩，若 xx 在排队，则事件成功执行，输出 OK； 否则输出 Error 并忽略这个事件。

「YAC Round 9」《东方妖精武踏会》

解题思路 set\text{set} 模拟

我们先整理一下需要维护的东西：

  • 当前处在队列中的人，并且需要维护顺序。

  • 当前正在玩游戏的人。

  • 每个人是否在排队 / 玩游戏。

本题的主要难点在于 leave 的实现，队列中的任意位置的人都可以离开队列。 因此，我们不得不采用可以删除任意位置元素的数据结构，但同时我们有需要维护每个人的顺序。故我们考虑用 set\text{set} 存储每个人的姓名并赋予一个编号，根据编号的大小升序维护这个队列中的所有人。

我们可以定义每个人的编号为：当前队列中最后一个人的编号 + 1\text{+ 1} （若队列先前为空，我们可以定义这个第一个加入队列的人的编号为 11）。set\text{set} 存储一个包含姓名和这个编号的结构体，重载一下 << 运算符即可维护队列中人的顺序。

对于每个人是否在排队 / 玩游戏，只需要开两个 map\text{map} 记录一下即可。对于是否在排队，我们需要记录一下其编号（主要是为了方便删除操作）；对于是否在玩游戏，只需要记录是否在玩即可。

同时，在每局游戏开始时，我们还需要将先前玩游戏的人先加入队列，再让队列的前两个或一个人上场。故我们可以用一个数组暂存每局游戏开始时上场的人的名字（包括人数）。

更具体的细节见代码注释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include<bits/stdc++.h>
using namespace std;

#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)

struct node{
    string s;
    int id;    // 按照排队编号维护顺序
    bool operator < (const node &b) const { return id < b.id; } 
};

set<node> q;   // 维护队列
unordered_map<string, int> inq;  // 维护在排队 及其 排队编号
unordered_map<string, bool> ing; // 维护是否在游玩

inline bool try_insert(string s){
    if(inq[s] || ing[s]) return false; // 如果在排队 或者 在游玩
    int id = 1;
    if(q.size()){
        auto it = q.end();   // 最后一个迭代器
        it -- ;              
        auto [t, pre] = *it; // 取队尾的人的编号
        id = pre + 1;        // 队尾编号 + 1
    }
    inq[s] = id;             // 维护每个人编号
    q.insert(node{s, id});   // 加入队列
    return true;
}

inline bool try_erase(string s){
    if(!inq[s]) return false;  // 如果不在排队 无法删除（包括正在玩的人）
    q.erase(node{s, inq[s]});  // 离队
    inq[s] = 0;                // 编号置为0
    return true;
}

string t[2];  // 存储每场玩游戏的人
int num;      // 每场玩游戏的数量

inline void try_start(){
    for(int i = 0; i < num; i ++ ){  // 上一场游戏的人重新加入到队尾
        ing[t[i]] = false;  
        try_insert(t[i]);   
    }
    num = min(2, (int)q.size());    
    if(!num){ 
        cout << "Error" << "\n";     // 没有人上游戏
        return;
    }
    for(int i = 0; i < num; i ++ ){
        auto [cur, id] = *q.begin(); // 进入游戏的玩家
        t[i] = cur;                  // 暂存这局玩游戏的人
        try_erase(cur);              // 从队列中删除（因为玩游戏的人不能离开，为了后续正确执行leave操作）
        ing[cur] = true;             // 在玩游戏
        cout << cur << " ";
    }
    cout << "\n";
}

int n;
string op, s;

int main(){
    ios;

    cin >> n;
    while(n -- ){
        cin >> op;
        if(op[0] == 'a'){
            cin >> s;
            cout << (try_insert(s) ? "OK" : "Error") << "\n";
        }else if(op[0] == 'l'){
            cin >> s;
            cout << (try_erase(s) ? "OK" : "Error") << "\n";
        }else{
            try_start();
        }
    }

    return 0;
}

E 幽雅地绽放吧，墨染之樱

题意描述

构造一棵树满足如下条件：

  • 一共有 nn 个节点

  • 满足 mm 个限制条件，其中第 ii 个限制条件可以为 (ui,vi)(u_i, v_i)：表示节点 uiu_i 和 viv_i 之间的唯一最短路径上 恰好有两条边 。

「YAC Round 9」幽雅地绽放吧，墨染之樱

解题思路 构造 + 并查集

节点 uu 和 vv 之间的路径恰好有两条边，也就是说，uu 和 vv 之间有且仅有一个中间节点。 我们可以先假定对于任意的限制 (ui,vi)(u_i, v_i) ，都存在一个待确定的中间点使其成立。

假设有一个限制 (1,2)(1, 2) 和另一个限制 (1,3)(1, 3)，此时节点 1,2,31, 2, 3 会不可避免地连到一个连通块中，而我们可以发现，这些连通块内的点都可以共享一个中间节点（后续称之为中心），使得连通块中所有的限制条件都成立（呈现出一个菊花图的模样）。

故我们可以用并查集先求出所有的连通块，每个连通块都有一个待确定的中心（呈现出若干个菊花图）。

那么，如何使得这多个菊花图连成一颗树，同时还能够使得所有限制条件依旧成立呢？

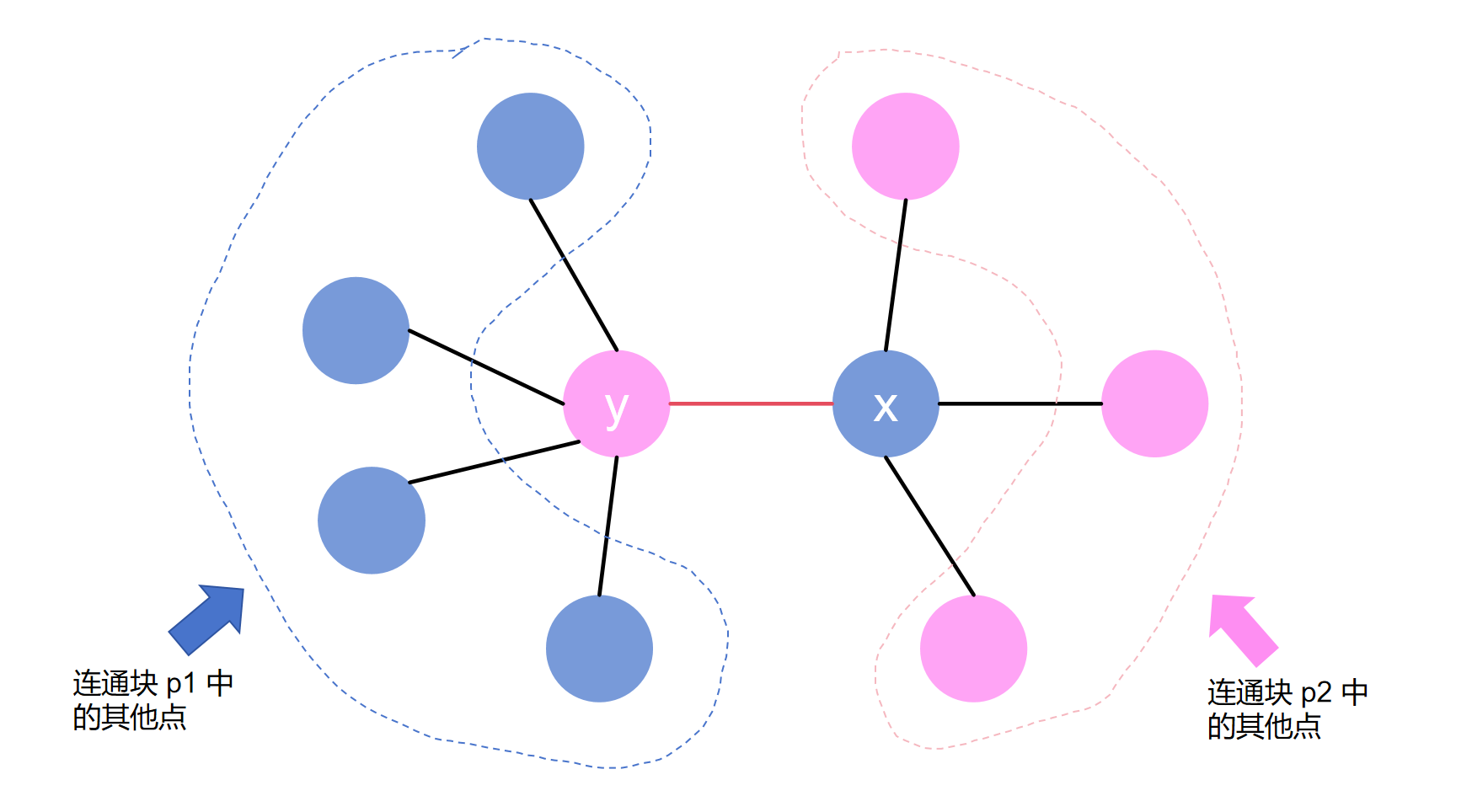
  • 如果有两个及以上的连通块（菊花图），那么一定有解。我们可以先任选两个连通块，并且在这两个连通块中各自任选一个点作为 对方连通块的中心，然后在两个选择的点之间再连一条边。假设选择的两个连通块为 p1p_1 和 p2p_2，在 p1p_1 中任选的一个节点为 xx，在 p2p_2 中任选的一个节点为 yy，作为对方的中心。构造出来的样子如图所示：

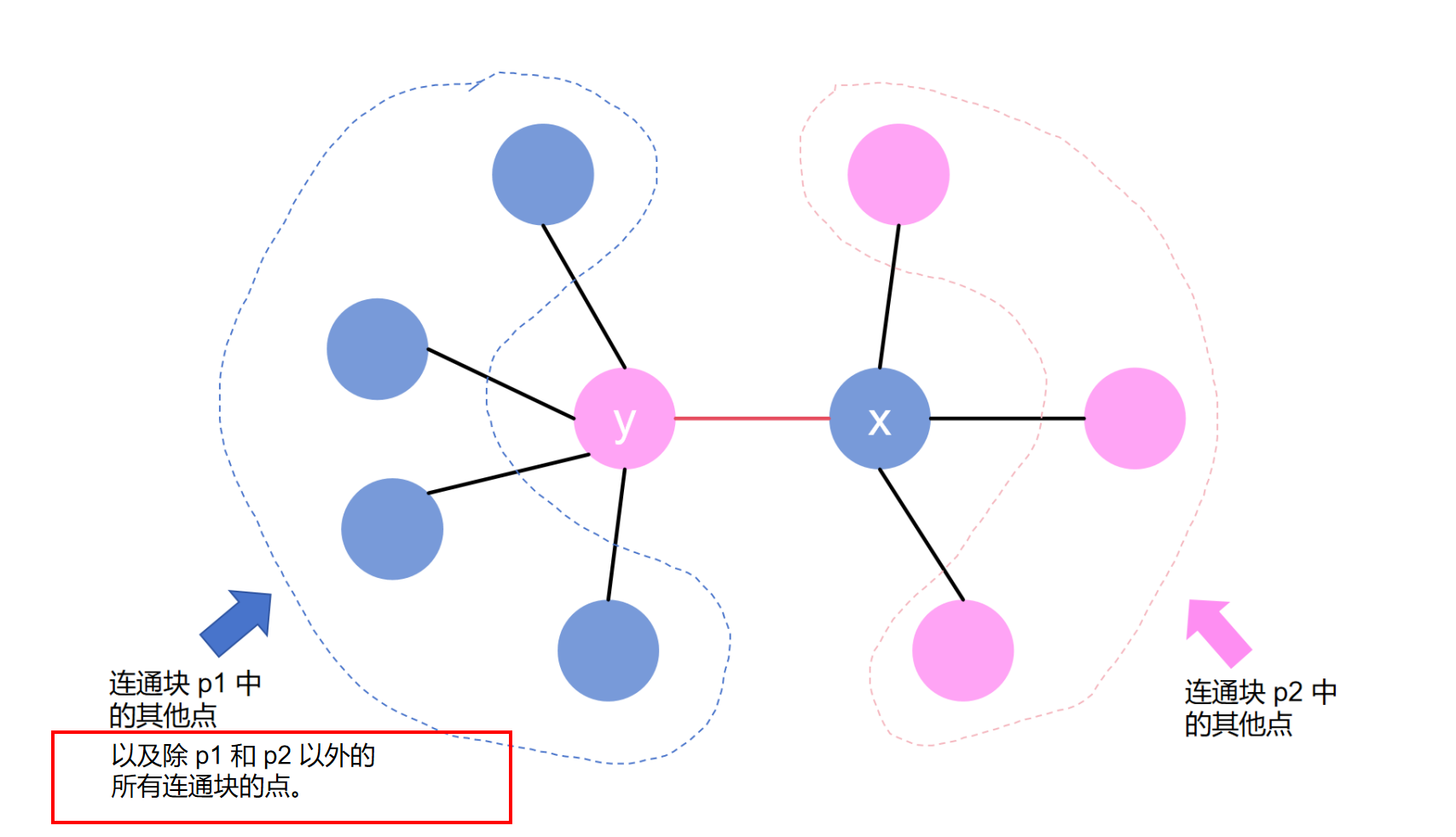
    然后，考虑处理剩下的连通块（菊花图）。而此时我们发现，只要任意选择一个先前任选的两个连通块中的一个节点作为上下所有连通块的中心即可，也就是说，选择连通块 p1p_1 和 p2p_2 中的任意一个节点，然后作为其余所有连通块共享的中心。这样就可以满足所有的限制条件了。为了方便，我们可以直接选择先前在 p1p_1 中选择的节点 xx 。

    基于之前那张图，我们最终构造出来的样子如下图所示：

  • 如果只有一个连通块，当只有一个节点 11，此时没有任何限制条件，也是有解的，只不过这个树没有边而已；否则，一定无解。可以想象一下，总共只有一个连通块（菊花图），我们至少需要一个节点来作为这个连通块的中心节点，然而此时所有点都在这个连通块上，没有剩余点可以用了，故无解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;

#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
const int N = 3e5 + 10;

int fa[N]; // 并查集
int find(int x){ return fa[x] == x ? x : fa[x] = find(fa[x]); }
void merge(int x, int y){ fa[find(x)] = find(y); }

int main(){
    ios;

    int T; cin >> T;
    while(T -- ){
        int n, m; cin >> n >> m;
        for(int i = 1; i <= n; i ++ ) fa[i] = i;
        for(int i = 1, u, v; i <= m; i ++ ) cin >> u >> v, merge(u, v);
        
        int cnt = 0;      // 连通块（菊花图）个数
        vector<int> v;    // 任选的两个连通块的节点
        for(int i = 1; i <= n; i ++ )
            if(fa[i] == i){
                cnt ++ ;
                if(v.size() < 2) v.push_back(i);
            }

        if(cnt == 1){     // 如果只有一个菊花图 没有其他点可以作为中心 
            cout << (n == 1 ? "Yes" : "No") << "\n"; // 特判只有一个节点
            continue;
        }

        cout << "Yes" << "\n";
        cout << v[0] << ' ' << v[1] << "\n"; // 任选的两个点连一条边
        for(int i = 1; i <= n; i ++ ){
            if(i == v[0] || i == v[1]) continue;
            if(find(i) == v[0]) cout << v[1] << ' ' << i << "\n";
            else cout << v[0] << ' ' << i << "\n"; 
        }
    }

    return 0;
}

F 咏唱光芒

题意描述

给定一个 nn 个点 mm 条边的无向图。有 qq 次询问，每次询问两个点 x,yx, y，问两点之间所有的简单路径上最小边权的最大值。「YAC Round 9」咏唱光芒

解法一 kruskal\text{kruskal} + 启发式合并

不难想到的方法是，将边权从大到小排序，对于每个询问 (x,y)(x, y)，将边依次插入图中，直到 xx 和 yy 连通时的那条边就是两点之间所有简单路径的最小边权的最大值。这是典型的 kruskal\text{kruskal} 求最小/最大生成树方法。但是有很多组询问，每组询问都进行 kruskal\text{kruskal} 建树，显然是不可取的。

可以发现本题允许离线处理询问，故我们可以考虑 启发式合并 来进行优化。

利用启发式合并的思想，我们将每个询问挂在它的两个端点上，然后在合并两个连通块时，处理较小的连通块中的询问，并将较小连通块连接到较大连通块上（OI Wiki 启发式合并）。

我们假设较大的连通块为 fxfx，较小的连通块为 fyfy：

  • 若当前关于 fyfy 询问的 另一个端点已经和 fxfx 连通，那么当前枚举到的边的长度就是这个询问的答案。

  • 否则，这条边还不能使得这个询问成立。故此时我们要把这个询问 转移到
    fxfx 中    ，之后在进行再处理。

由于启发式合并算法每次合并到较大连通块的特点，询问是不会重复处理的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<bits/stdc++.h>
using namespace std;

#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
typedef pair<int, int> pii;
const int N = 1e5 + 10, M = 3e5 + 10;

struct node{ int u, v, w; }e[M];
vector<pii> query[N];
int fa[N], sz[N], ans[N], n, m, q;

int find(int x){ return fa[x] == x ? x : fa[x] = find(fa[x]); }

int main(){
    ios;

    cin >> n >> m >> q;
    for(int i = 1, u, v, w; i <= m; i ++ ){
        cin >> u >> v >> w;
        e[i] = node{u, v, w};
    }

    for(int i = 1, u, v; i <= q; i ++ ){
        cin >> u >> v;
        query[u].emplace_back(v, i);
        query[v].emplace_back(u, i);
    }

    for(int i = 1; i <= n; i ++ ) fa[i] = i, sz[i] = 1;
    sort(e + 1, e + m + 1, [](node &a, node &b){ return a.w > b.w; });
    
    for(int i = 1; i <= m; i ++ ){ // kruskal最大生成树
        auto [x, y, w] = e[i];
        int fx = find(x), fy = find(y);
        if(fx == fy) continue;
        if(sz[fx] < sz[fy]) swap(fx, fy);       // 合并到较大的连通块
        for(auto &[u, id] : query[fy]){         // 处理较小连通块上的询问
            if(find(u) == fx) ans[id] = w;      // 连通 答案为当前的边长度
            else query[fx].emplace_back(u, id); // 否则转移到大连通块
        } 
        fa[fy] = fx, sz[fx] += sz[fy];
    }

    for(int i = 1; i <= q; i ++ ) cout << (ans[i] ? ans[i] : -1) << "\n";

    return 0;
}

解法二 kruskal\text{kruskal} + 倍增 LCA\text{LCA}

我们要求的是两点之间所有简单路径中最小边权的最大值，故我们可以先用 kruskal\text{kruskal} 构建出最大生成树，所有的 (x,y)(x, y) 询问的答案一定是这颗最大生成树上两点之间唯一最短路径上的最小边权。

树上两点之间最短的路径，不难想到两点的 LCA\text{LCA}（最近公共祖先），考虑用 倍增 求 LCA\text{LCA} 的同时维护两点到祖先的最小边。每当询问一对点 (x,y)(x, y) 时，询问的答案就是 xx 和 yy 到 lca(x,y)lca(x, y) 的最小边。

P3379 【模板】最近公共祖先（LCA）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<bits/stdc++.h>
using namespace std;

#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
typedef pair<int, int> pii;
const int N = 1e5 + 10, M = 3e5 + 10, inf = 0x3f3f3f3f;

int n, m, q, fa[N];
struct node{ int u, v, w; }edge[M];
vector<pii> e[N];

int find(int x){ return fa[x] == x ? x : fa[x] = find(fa[x]); }

void kruskal(){ // 最大生成树
    for(int i = 1; i <= n; i ++ ) fa[i] = i;
    sort(edge + 1, edge + m + 1, [](node &a, node &b){ return a.w > b.w; });
    for(int i = 1; i <= m; i ++ ){
        auto [u, v, w] = edge[i];
        int fx = find(u), fy = find(v);
        if(fx == fy) continue;
        fa[fy] = fx;
        e[u].emplace_back(v, w);
        e[v].emplace_back(u, w);
    }
}   

int f[N][22], mn[N][22], d[N]; // 倍增求lca并维护最小边

void bfs(int src){
    queue<int> q;
    q.push(src);
    d[src] = 1, f[src][0] = src, mn[src][0] = inf;

    while(q.size()){
        int u = q.front();
        q.pop();

        for(auto &[v, w] : e[u]){
            if(!d[v]){
                q.push(v);
                d[v] = d[u] + 1, f[v][0] = u, mn[v][0] = w;

                for(int k = 1; k <= 20; k ++ ){
                    f[v][k] = f[f[v][k - 1]][k - 1];
                    mn[v][k] = min(mn[v][k - 1], mn[f[v][k - 1]][k - 1]);
                }
            }
        }
    }
}

int lca(int a, int b){
    if(find(a) != find(b)) return -1; // 不连通
    int res = inf;
    if(d[a] < d[b]) swap(a, b);

    for(int k = 20; k >= 0; k -- )
        if(d[f[a][k]] >= d[b]){
            res = min(res, mn[a][k]);
            a = f[a][k];
        }

    if(a == b) return res;

    for(int k = 20; k >= 0; k -- )
        if(f[a][k] != f[b][k]){
            res = min({res, mn[a][k], mn[b][k]});
            a = f[a][k], b = f[b][k];
        }

    return min({res, mn[a][0], mn[b][0]});
}

int main(){
    ios;

    cin >> n >> m >> q;
    for(int i = 1, u, v, w; i <= m; i ++ ){
        cin >> u >> v >> w;
        edge[i] = node{u, v, w};
    }

    kruskal();

    for(int i = 1; i <= n; i ++ ) if(!d[i]) bfs(i);

    while(q -- ){
        int u, v; cin >> u >> v;
        cout << lca(u, v) << "\n";
    }

    return 0;
}
咏唱光芒 > YAC 扬州大学算法练习赛
#C++ #算法 #算法竞赛 #Luogu #YAC
2024 YAC Round 9 题解
https://marisamagic.github.io/2024/12/14/YAC_Round_9/
作者
MarisaMagic
发布于
2024年12月14日
许可协议